CSR:
Small: Provably Correct Design of Observation for Fault Diagnosis and
State Estimation under Privacy and Network Constraints
(NSF Project CNS-1816369)
Summary
During the operation of complex
cyber-physical systems, operation planning and control need to be performed
using limited available information. There are two reasons for this limitation.
First, privacy issues may limit what information can be shared. Second, in a
complex cyber-physical systems, not all state information can be measured, and
the communication between subsystems may be limited.
These limitations give rise to a
number of fundamental research questions as follows. Question 1: Can the right
inference be made using the available state information, for the purposes of
fault diagnosis and state estimation? Question 2: What state measurement or
observation can be made available to facilitate the answer to Question 1
without violating privacy constraints? Question 3: When the information is
transmitted through a non-ideal communication network, resulting in
transmission delay or limited bandwidth, how does it affect Questions 1 and 2
above?
In this project we develop a
framework that provides us with provably correct answers to all of the
questions above. Our framework is a model-based approach to obtain provably
correct methods for designing state measurement/observation that meets the need
for fault diagnosis and state estimation while meeting privacy and network
constraints. This is a hard problem especially for complex systems that are
marked by hybrid behavior (i.e. involving both discrete and continuous
dynamics), high dimensional state space, and nonlinear dynamics.
Our approach is based on
approximating the behavior of the system, i.e. the set of all possible
execution trajectories, with a behavior with finitely many trajectories that
are obtained from numerical simulations. This approximation can be done with
controllable precision, resulting in a trade-off between the complexity of
generating the approximation and its precision. In this framework, state
measurement/observation are performed by online monitors that implement dense
time temporal logic formulae. The formulae are defined over measured variables
(provided by sensors) and logical predicates over these variables (provided by
software-defined sensors). We also develop a framework with which state
observers will be designed on top of the online monitors.
In case the computation for creating the finite
approximate behavior is prohibitively costly, we will also explore the use of
randomized algorithms. We propose to develop a method to speed-up known
randomized algorithms by exploiting the local properties of the generated
samples.
Publications (only published peer-reviewed ones)
[1] Z. Xu, S. Saha, A. A. Julius,
Provably Correct Design of Observations for Fault Detection with Privacy
Preservation. In Proc. IEEE Int. Conf. Decision and Control, Melbourne, Australia, 2017.
[2] M. H. Jahnes, D. J. Glowny,
T. A. Spafford, J. L. Clough, E. S. Herkenham, W. Wu, A. A. Julius. Generating
Enthusiasm for Mathematics Through Robotics. In Proc. ASEE Annual Conference
and Expositions, Columbus,
Ohio, 2017.
Results
Application in privacy and fault detection in smart buildings.
Recently, we applied our framework on a model of the HVAC control in a
smart building. The model is in the form of a switched dynamical
systems consisting of differential equations that govern the evolution
of the temperature and humidity in a room as affected by their
environmental counterparts and the room occupancy. The four
states of the room are empty-normal, occupied-normal, empty-faulty, and
occupied-faulty as shown in Fig. 1. Fault is represented as an open
window that increases the thermal and humidity loads to the HVAC
system. Similarly, room occupancy results in increasing thermal and
humidity loads. To make the problem more interesting, we choose the
model parameters such that the steady-state temperatures of the
occupied-normal and empty-faulty modes are the same. We analyze the
model and found that we can use the room temperature signal to detect the fault and to infer about the room occupancy. However, we are interested in figuring out if we can construct an observation that can be used to detect the fault but oblivious to the change in occupancy,
because of privacy concern. Such observation can be constructed as an
online monitor that implements a temporal logic formula that is
constructed based on the the simulated trajectories of the model. The
formula (not unique) that we computed reads: “(Between 160 and 180 s
the temperature is always above 290.75) OR (between 0 and 20 s the
temperature is sometime below 290.516 AND between 39 and 65 s the
temperature is sometime above 290.525 AND between 122 and 161 s the
temperature is sometime below 290.625)”
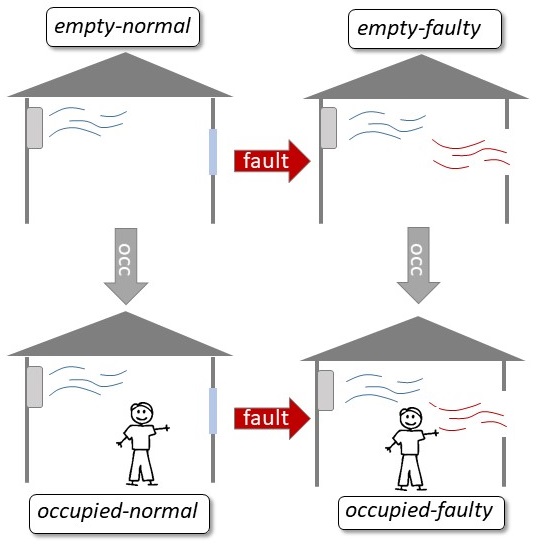
Fig. 1. Four modes of operation of the HVAC control system in a smart building.
Educational Outreach.
This project supported Engineering Ambassadors, who created and
presented STEM modules to K-12 students in the Capital Region of NY
State. This year, we wrote and presented a paper at the 2017 ASEE
Annual Conference in Columbus, OH. The paper presents data collected
from our outreach activities at Berlin Junior/Senior High School in
Berlin, NY and Lansingburgh High School in Troy, NY. The outreach
activity was focused on generating enthusiasm for mathematics through
robotics. Participants of these programs were asked to fill out a
questionnaire before and after they take part in the program. The
questionnaire consists of seven questions:
1. I enjoy doing activities within the area of robotics.
2. I enjoy doing activities within the subject of engineering.
3. I enjoy the subject of mathematics.
4. I enjoy the subject of science.
5. I enjoy doing activities like coding or computer science.
6. Mathematics is important when learning robotics.
7. The Engineering Design Process is an important tool for solving challenges.
The
responses to the questionnaires are summarized in Fig. 2. To summarize,
there is a statistically significant (p<0.05 in a paired t-test)
increase in the participants' responses to the questions is all cases,
except in the cases of Questions 3 and 4 in Lansingburgh High School.
For these cases, however, we still observe a slight increase in the
responses (p=0.06 and p=0.22, respectively).
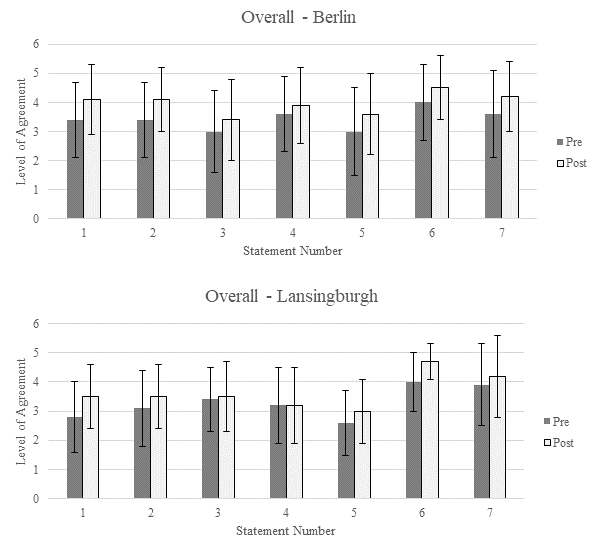
Fig.
2. Survey results from our educational outreach activities showing
statistically significant positive impacts on the participants.
Any opinions, findings, and conclusions or recommendations
expressed in this material are those of the authors and do not necessarily
reflect the views of the National Science Foundation.




